Regra 9: Uma restrição adequadamente aplicada a um corpo (sem super restrição) possui o efeito de remover um dos graus de liberdade rotacionais desse corpo. O grau de liberdade rotacional removido é aquele sobre o qual a restrição exerce um momento. Um corpo restringido por n restrições possuirá 6-n graus de liberdade rotacionais, cada qual posicionado de modo que nenhuma restrição exerça momento sobre ele. Em outras palavras, cada grau de liberdade rotacional interceptará todas as restrições.
Esta regra é uma extensão das regras 4 e 5 que fornece um meio de testar a existência de super restrições e sub restrições. O primeiro teste é simplesmente contar o número de restrições. Pode-se generalizar para corpos não rígidos aumentando o número dos graus de liberdade do corpo livre (C) com a soma dos f graus de liberdade flexíveis. O número de graus de liberdade independentes requeridos para a restrição exata de um corpo é n = 6 + f – d, onde d é o número de graus de liberdade desejados. O segundo teste é necessário para se determinar se as restrições são independentes. A remoção de uma restrição redundante não afetará o número de graus de liberdade sobre os quais as outras restrições atuam. O sistema é exatamente restringido se a remoção de uma simples restrição aumentar o número de graus de liberdade em um. A figura 38 mostra um exemplo específico sobre isto e a tabela de restrições ortogonais da figura 36 mostra outros exemplos através das mudanças observadas entre células adjacentes.
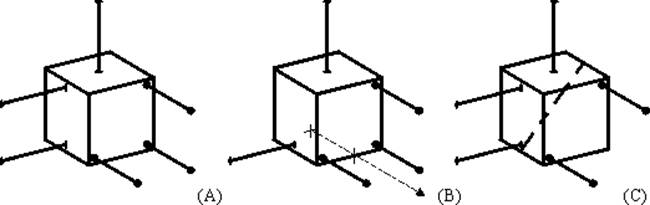
Para testar se qualquer uma das restrições em 38(a) é independente, remova qualquer restrição simples e verifique se restou algum grau de liberdade. A restrição removida em 38(b) deixa de exercer um momento resistivo ao longo do eixo mostrado, e nem qualquer das outras restrições. O mesmo ocorre em 38(c) e nos outros casos.

Figura 38 – Teste de restrições redundantes.