Regra 6: Qualquer conjunto de restrições cujas linhas de restrição interceptem um conjunto independente e completo de eixos de rotação, é funcionalmente equivalente a qualquer outro conjunto de restrições cujas linhas de restrição interceptem o mesmo ou equivalente conjunto de eixos de rotação. Isso é verdadeiro para pequenos deslocamentos e quando cada conjunto contém o mesmo número de restrições independentes.
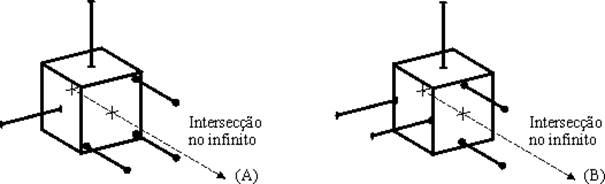
Essa regra é uma extensão da regra 3, a equivalência funcional de qualquer par de restrições possuindo o mesmo centro instantâneo, baseado na regra 4, a generalização do centro de rotação para um eixo rotacional. A regra é mais útil e significativa quando as restrições forem quatro ou mais, já que pelo menos dois pares de restrições são necessários para definir um eixo de rotação. Os exemplos mostrados na figura 35 são funcionalmente equivalentes (para pequenos deslocamentos) entre si e ao exemplo da figura 32. Isso ocorre porque todas as cinco restrições interceptam o mesmo eixo rotacional.

Figura 35 – Restrições aplicadas, deixando um único grau de liberdade restante, uma rotação em torno do centro do cubo.
Blanding, 1992, desenvolveu uma tabela contendo todas as possíveis restrições ortogonais envolvendo de uma a seis restrições. A figura 36 mostra a tabela de restrições ortogonais, que fornece uma excelente base para o início de um projeto com restrição exata. Um número infinito de configurações não ortogonais é possível de ser obtido com base nessas configurações básicas.
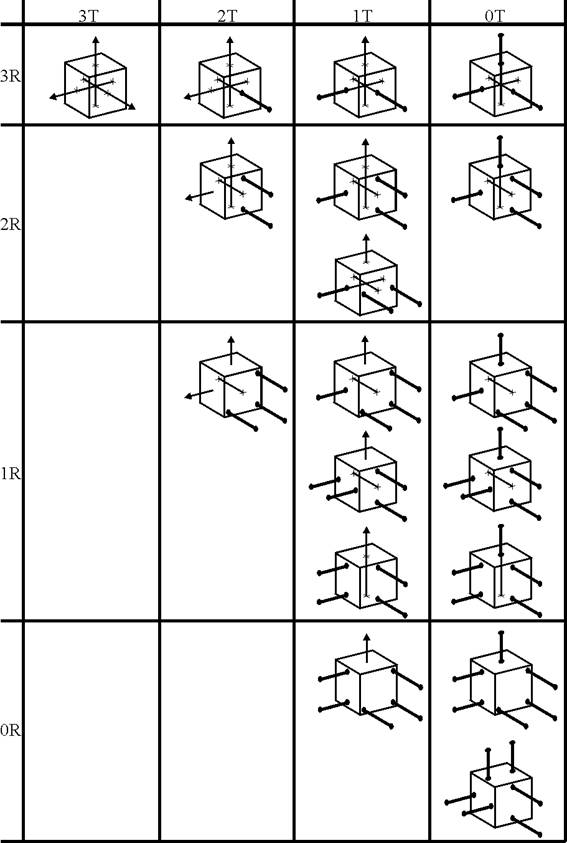
Figura 36 – Matriz dos graus de liberdade rotacional (linhas de centro) e translacional (setas) desejados, mostrando todos os possíveis arranjos de restrição ortogonal [Blanding, 1992].