Regra 5: Uma restrição aplicada a um corpo remove o grau de liberdade rotacional sobre o qual essa restrição executa um momento .
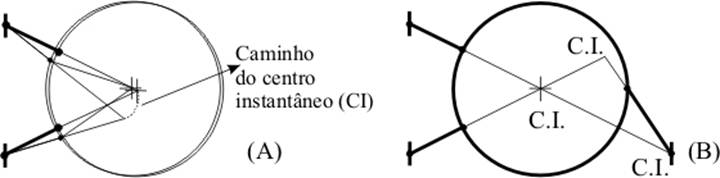
Para restringir um grau de liberdade rotacional (o que inclui as translações por equivalência), a restrição deve reagir como um momento em torno do eixo de rotação. A restrição vai satisfazer esse requisito se a linha de restrição não interceptar o eixo de rotação e se a linha de restrição não é paralela ao eixo de rotação. Uma exceção à primeira condição resultará num braço de alavanca com comprimento zero. Uma exceção à segunda condição resultará num momento que não possui componente ao longo do eixo de rotação. A figura 33 mostra a adição de uma terceira restrição para prevenir a rotação do círculo em torno do seu centro. Cada restrição evita a rotação em torno de um centro instantâneo formado pelo outro par de restrições, então esses três graus de liberdade estão exatamente restritos. Os eixos dos três graus de liberdade restantes vão interceptar as três restrições, conforme a regra 4. Se acontecer de as três restrições se posicionarem no plano da figura, então os eixos de rotação livre também irão.
A liberdade rotacional do círculo é em torno do centro em 33(a) e é restringida em 33(b) pela adição de uma restrição que reage com um momento em torno do centro. Cada restrição reage com um momento em torno de um centro instantâneo formado pelo outro par de restrições.

Figura 33 – Centro instantâneo com três restrições.
O comprimento do braço de alavanca, representado pela linha perpendicular da linha de restrição ao eixo rotacional restringido, é uma medida relativa da eficiência daquela restrição. Se o objetivo é encontrar um projeto balanceado, uma medida eficiente é obter os braços de alavanca com o mesmo comprimento. Isto leva a uma lei simples a ser aplicada em problemas no plano; posicionar as linhas de restrição de modo a formarem um triângulo eqüilátero, como mostrado na figura 34. Muitos problemas tridimensionais possuem uma natureza planar, o que ajuda muito na sua visualização.
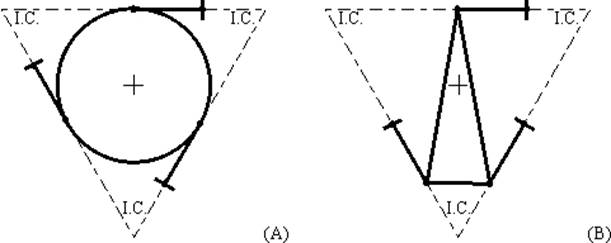
Figura 34 – Arranjo eqüilátero das restrições.
Um arranjo eqüilátero das restrições sempre levará a um balanço otimizado da rigidez. Em 34(a) o centro de rigidez coincide com o centro do círculo, então a rigidez horizontal é igual à vertical. Em 34(b) não há a coincidência, então a rigidez horizontal será diferente da vertical.