Regra 3: Qualquer par de restrições cujas linhas de restrição se interceptam num dado ponto é funcionalmente equivalente a qualquer outro par no mesmo plano cujas linhas de restrição se interceptam no mesmo plano. Isto é verdadeiro para pequenos movimentos onde as duas restrições se referem a linhas de restrição distintamente diferentes.
A intersecção descrita por essa regra é um centro de rotação instantâneo ou simplesmente um centro instantâneo. A redução de um par (ou trio) de restrição a um centro instantâneo é uma ajuda conceitual e visual muito importante no campo da cinemática. Entretanto, devemos diferenciar entre um ponto estacionário que está sobre ou relativo a um corpo restringido e o centro estacionário que leva momentaneamente a esse ponto. O ponto no corpo pode possuir somente movimento instantâneo perpendicular ao plano formado pelas duas restrições. Neste plano o ponto aparecerá estacionário para pequenos movimentos enquanto o centro instantâneo aparecerá se movendo com o movimento das direções de restrição. Qualquer par de restrições que atue nesse plano e que intercepte o mesmo ponto permitirá o aparecimento do mesmo movimento instantâneo daquele ponto no corpo. Entretanto, o movimento do centro instantâneo deve ser distinto. Qualquer outro ponto no corpo deverá ter uma componente tangencial adicional de movimento instantâneo em torno do centro instantâneo, como mostrado na figura 31.

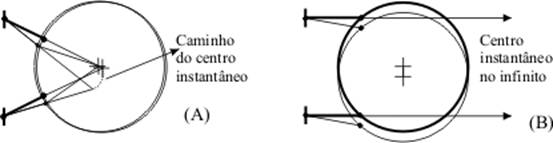
Figura 31 – Posição do centro instantâneo.
Em 31(a), o centro instantâneo está momentaneamente localizado no centro físico do círculo. O centro instantâneo se move para baixo enquanto o círculo rotaciona aproximadamente sobre seu centro físico. Em 31(b), o centro instantâneo está no infinito e o círculo inicialmente translaciona para baixo.
A condição de que duas linhas de restrição sejam distintamente diferentes requer mais explicações, já que leva a um conceito chave. Se duas restrições estão alinhadas, então não definem um plano e essa regra passa a não funcionar. O resultado físico passaria a ser um grau de liberdade super restringido, ao invés de dois graus de liberdade restringidos. Um caso aceitável, entretanto, é a existência de duas restrições paralelas, definindo um plano. Como indicado na figura 31(b) devemos considerar linhas de restrição paralelas que se interceptam no infinito, desde que as trajetórias apareçam a uma certa distância. Um objeto que rotacione em torno de um centro distante aparenta possuir translação, como um navio, que rotaciona com relação ao centro da terra. Por essa ótica, podemos dizer que, conceitualmente, as três translações e as três rotações são equivalentes a seis graus de liberdade de rotação, onde três eixos de rotação estão no infinito.