Regra 12: Quando os componentes são conectados em série (cascata), há a adição dos graus de liberdade. Quando os componentes são conectados em paralelo, há a adição de restrições.
Podem ser utilizados dois princípios familiares para explicar a regra 12.
Princípio 1: A deformação equivalente de molas montadas em série é a soma das suas deformações individuais.
Princípio 2: A rigidez equivalente de molas montadas em paralelo é a soma da rigidez individual de cada uma.
Estes princípios podem ser aplicados tanto para molas com um grau de liberdade, quanto outras estruturas e molas de quaisquer dimensões, onde a constante de mola torna-se uma matriz simétrica. Devemos considerar um grau de liberdade como sendo um termo dominante na matriz de deslocamento, já que sua origem é a elasticidade de uma placa flexível ou o movimento de um mancal. Similarmente, deve-se considerar uma restrição como sendo um termo dominante na matriz de rigidez. O fundamento para a regra 12 é que os termos dominantes em matrizes individuais permanecem dominantes no processo de adição. Conseqüentemente, os graus de liberdade dominam os processos de combinação em série enquanto as restrições dominam os processo de combinação em paralelo. Isso expõe uma sutileza não aparente na regra 12, que é como lidar com graus de liberdade e restrições redundantes. Esses pontos serão exemplificados a seguir, primeiro numa combinação em série e em seguida numa combinação em paralelo.
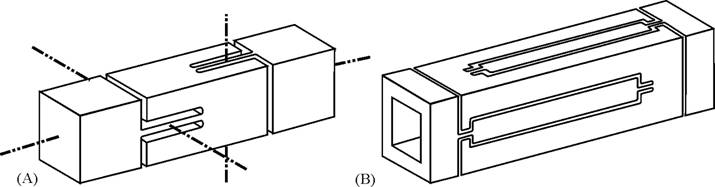
A figura 40(a) mostra uma combinação em série de duas placas que ocupam uma linha de restrição comum. Uma má interpretação da regra 12 levaria à conclusão de que essa série de placas, cada qual com três graus de liberdade, se combinaria formando um total de seis graus de liberdade, sem restrições. O deslocamento axial combinado ao longo da linha de restrição permanece algumas ordens de grandeza mais rígido do que nas outras direções, então ainda é uma restrição. Da mesma forma, as placas ocupam um eixo rotacional comum que resulta num grau de liberdade redundante. A combinação deve ter duas vezes o deslocamento, mas funcionalmente continua sendo um único grau de liberdade. Nas direções restantes a regra 12 é aplicada sem confusão já que os quatro graus de liberdade combinam com as quatro restrições. Assim, a combinação em série de duas placas de flexão fornece três graus de liberdade rotacionais diferentes e uma restrição axial.
A figura 40(b) mostra um elemento flexível mais elaborado, que possui combinações em série e em paralelo de placas. Essa configuração é vazada para prevenir o aparecimento de um circuito fechado entre os graus de liberdade desejados. Sua simetria leva a restrições redundantes. O componente poderia funcionar da mesma forma sem as restrições redundantes, mas sacrificaria a sua rigidez ao longo da sua linha de restrição.

Figura 40 – Elementos flexíveis.
Resumindo, a maneira correta de interpretar a regra 12 exige a consciência sobre as direções envolvidas. Para uma combinação de elementos em série, os graus de liberdade combinados irão amarrar a união de espaços dimensionais amarrados pelos graus de liberdade das partes individuais; enquanto, as restrições combinadas vão amarrar a intersecção dos espaços amarrados pelas restrições das partes individuais. Para uma combinação de elementos em paralelo, as restrições combinadas vão amarrar a união dos espaços dimensionais amarrados pelas restrições das partes individuais; enquanto os graus de liberdade combinados irão amarrar a intersecção de espaços amarrados pelos graus de liberdade das partes individuais.
As doze regras de Blanding são importantes para entender e referenciar quando for a hora de projetar um sistema ou mecanismo restrito. Em muitos casos é possível iniciar com um projeto básico, como com um dos acoplamentos cinemáticos convencionais, mas como a figura 41 mostra, alguns casos podem ser produzidos a partir da tabela de restrições ortogonais da figura 38, associado com um conhecimento básico de elementos de restrição, como esferas encaixadas em ranhuras em V. Leve em consideração que restrições e eixos de intersecção ortogonais são simplificações artificiais utilizadas para produzir uma tabela simples e concisa. Em 41(a), uma esfera montada num assento tetraédrico fornece três restrições; Uma esfera num V fornece duas restrições; e uma esfera num plano fornece a restrição restante. Em 41(b), três esferas, cada qual num V fornecem duas restrições. Em 41(c), três cilindros, cada qual num plano, fornecem duas restrições.
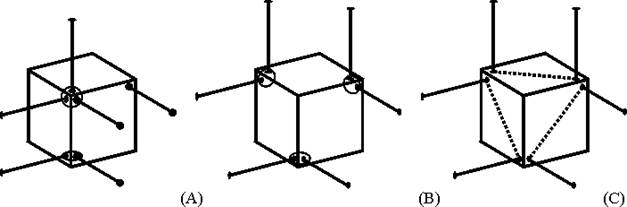
Figura 41 – Restrições de acoplamentos cinemáticos tradicionais.
Um conceito chave no projeto por restrições exatas é a relação entre as restrições aplicadas e os graus de liberdades restringidos um a um. Restrições redundantes podem ser adicionadas para aumentar a rigidez. Como conclusão pode-se dizer que o melhor projeto pode não ser aquele que possuir restrições exatas, mas deve ser iniciado dessa forma, de modo que a super-restrição seja totalmente considerada e prevista.