10 – Gerenciamento térmico
Uma das causas mais comuns da falta de repetitividade é a temperatura. Mais especificamente a causa é a mudança de temperatura com o tempo, que causa distorções térmicas no circuito estrutural das máquinas-ferramentas.
Para se ter um exemplo da influência da temperatura num sistema mecânico, considere-se uma barra de um metro feita em aço inoxidável. Os primeiros padrões de comprimento eram feitos com esse material. Se essa barra sofrer uma variação de temperatura de 1º C, dilatar-se-á num comprimento de 11 μm. Como as máquinas-ferramentas de precisão e ultraprecisão são projetadas para atingirem uma exatidão de posicionamento com valores 100 ou até 1000 vezes menores do que essa dilatação, fica evidente a importância das variações de temperatura numa máquina-ferramenta.
A temperatura padrão internacional, onde um objeto possui suas dimensões verdadeiras, é de 20º C. Isto implica que a distribuição de temperatura deve ser constante e uniforme até a peça. Por acordo internacional, a metrologia em qualquer outra temperatura contém erros termicamente induzidos, embora suas componentes sistemáticas possam ser reduzidas através de compensação. Os erros termicamente induzidos em máquinas de medição ou máquinas-ferramentas são usualmente mais significativos devido ao seu tamanho e complexidade. Donaldson, em 1979, descreveu uma série de métodos para aumentar a estabilidade térmica entre uma máquina e a peça. Os métodos geralmente seguem a ordem de passivo para ativo, o que deve ser considerado como a ordem preferida para qualquer projeto de máquinas. Esses métodos serão apresentados de forma resumida a seguir.
1 – Redução de sensibilidade
a) Projeto estrutural: Deve-se obter distribuições de temperatura simétricas através de estruturas simétricas para reduzir as distorções.
b) Materiais com baixo coeficiente de dilatação: Utilizar materiais com baixo coeficiente de dilatação para reduzir as variações na geometria devido às variações na temperatura.
2 - Gerenciamento de fontes de calor
a) Eliminar: Posicionar as fontes de calor necessárias fora do ambiente controlado e elimine as fontes de calor desnecessárias.
b) Reduzir: Utilizar componentes que dissipem menos calor.
c) Isolar: Prender o calor perto da fonte ou prevenir seu espalhamento na estrutura.
d) Evitar o espalhamento: Fluidos que removam calor de uma fonte isolada devem retornar diretamente para o sistema de controle de temperatura ao invés de ficar escoando sobre outros componentes sensíveis do sistema.
e) Manter as fontes de calor constantes: As fontes de calor necessárias no ambiente controlado, como a iluminação, devem permanecer constantes.
3 – Controle do ambiente da máquina
a) Controle de temperatura do ar da sala: Reduzir as variações de temperatura na máquina controlando a temperatura do ar em torno dela.
b) Isolamento da sala da máquina: Prevenir o vazamento de calor para dentro ou para fora da sala da máquina para reduzir as variações na temperatura do ar da sala.
c) Isolamento da estrutura: Controlar a temperatura no circuito de metrologia.
d) Controle da temperatura da peça: Usar o escoamento de um fluido com temperatura controlada sobre a peça para controlar sua temperatura. Considerar o efeito de aquecimento viscoso em escoamentos de fluidos em alta velocidade.
e) Isolar o operador da máquina: O corpo humano é equivalente a uma fonte de calor com aproximadamente 100 watts. Aplicações que demandam precisão exigem o uso de roupas especiais como as luvas.
4 – Compensar os desvios de medição
a) Compensação do crescimento do cabeçote: Usar um sensor de deslocamento adequado, como um transdutor capacitivo, para medir o crescimento axial do cabeçote e compensar a posição do eixo Z.
b) Temperatura do circuito de metrologia: Medir a temperatura no circuito de metrologia com sensibilidade e detalhamento suficientes para obter o erro e compensar as posições das guias.
A experiência tem mostrado que o controle de temperatura é a forma mais efetiva e confiável de reduzir os erros térmicos. Além disso, é um dos aspectos menos dispendioso de uma máquina-ferramenta de precisão e exige o emprego de pouco hardware adicional. O desafio de projeto é mostrar como obter controle suficiente para os menores custos.
Segundo Weck, 1980, as fontes de calor numa máquina-ferramenta podem ser divididas em fontes externas e fontes internas. As fontes externas de calor são:
a) Temperatura de objetos ao redor da máquina diferente da temperatura da máquina, unidades de refrigeração, paredes aquecidas, outras máquinas,...;
b) Irradiação solar;
c) Temperatura do meio ambiente que possa alterar a temperatura da máquina (ar, fluidos refrigerantes, lubrificantes,...);
As fontes internas de calor são:
a) Transmissão dos motores elétricos;
b) Atritos nos acionamentos e caixas de engrenagens;
c) Atrito nos mancais e guias;
d) Processo de usinagem (ação de corte, cavacos, peça).
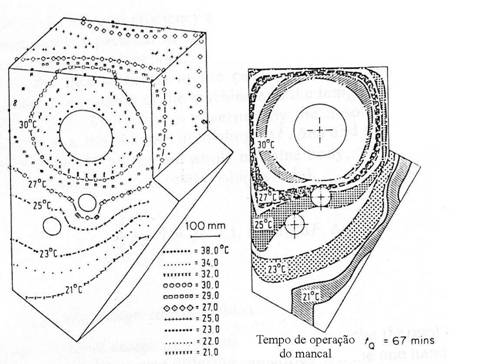
A figura 26 mostra as linhas isotérmicas de propagação de calor nas paredes de um assento de cabeçote de um torno de barramento inclinado. A geração de calor foi obtida após 67 minutos de operação ininterrupta do cabeçote da máquina. Em 26(a) está representada a propagação real coletada em ensaios e em 26 (b) é mostrada a simulação computacional feita para esta situação.

Figura 26 – Propagação de calor em um assento de cabeçote.
As relações de causa e efeito podem ser calculadas com um detalhamento considerável se forem utilizados modelos matemáticos simulados em softwares computacionais modernos (análises de elementos finitos e dinâmica dos fluidos computacional) e equações básicas da transferência de calor, mas para fazer isso, é necessário um considerável conhecimento sobre o projeto e o ambiente. Os dados obtidos a partir de sistemas já existentes ou testes específicos devem ser mais fáceis de se obter e justificar como válidos. Alguns modelos simples são apresentados em seguida para fornecer um melhor entendimento dos parâmetros importantes e sua relação com o problema de controle térmico (Holman,1976).
Suponha-se que uma barra sólida possua um gradiente de temperatura constante como expressado na equação 3. Quer-se calcular as rotações e deslocamentos locais para qualquer ponto na barra relativo ao plano fixo y-z mostrado na figura 27. O gradiente de deformação térmica é relacionado com o gradiente de temperatura pelo coeficiente de expansão térmica α. As rotações locais são obtidas pela equação 4 através da integração dos gradientes de deformação a partir de uma extremidade fixa. Os deslocamentos locais são obtidos pela equação 5 através da integração da diferença de temperatura ao longo do eixo x e pela integração das rotações em torno dos eixos y e z.
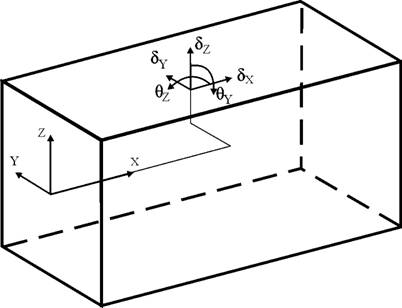
Figura 27 – Deslocamentos e rotações no ponto (x,y,z) relativos ao sistema fixo de coordenadas x-y-z e sujeito a um gradiente de temperatura constante.
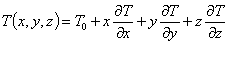 (3)
(3)
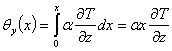
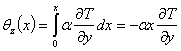 (4)
(4)
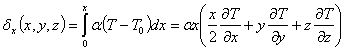
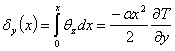
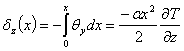 (5)
(5)
Freqüentemente é mais conveniente especificar um estado de fluxo de calor unidirecional (um fluxo de calor q dividido pela área A) do que um gradiente de temperatura. Por exemplo, a radiação solar está na ordem de 1 kW/ m2. O fluxo de calor através do material é igual ao gradiente de temperatura multiplicado pela condutividade térmica k. Assumindo que o fluxo de calor é uniforme e escoa em todas as direções x, y e z, o ponto deslocado no final da barra possui a mesma magnitude independentemente da direção do fluxo como mostram a equação 6 e a figura 28. A propriedade do material importante é a razão de expansão térmica pela condutividade α/k.
![]()
![]() (6)
(6)
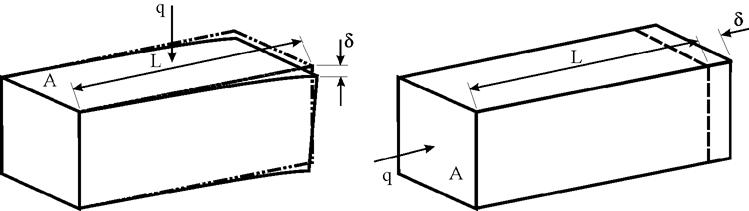
Figura 28 – Deslocamento na extremidade devido a um fluxo de calor uniforme especificado através de uma barra sólida.
Os problemas térmicos dependentes do tempo envolvem a massa térmica da estrutura interagindo com a transferência de calor por condução, convecção e radiação. Uma simplificação do problema leva a equações que descrevem cada tipo de transferência de calor separadamente. Começando com a condução, a equação de difusão unidimensional, mostrada na equação 7, fornece um importante grupo de propriedades dos materiais que dão uma medida do tempo necessário para o calor se difundir ou dissipar numa estrutura. O inverso desse grupo chamado de difusividade pode ser interpretado como a taxa de dissipação. A tabela 6 fornece a descrição dos símbolos.
![]() (7)
(7)
A taxa com a qual a estrutura muda a temperatura de forma significativa depende da transferência de calor nos arredores. Se a resistência térmica é pequena relativa à resistência de convecção e/ou radiação na sua superfície, então a equação 8 é uma aproximação razoável que descreve a constante de tempo do sistema τ. Ela expressa uma parte isotérmica da capacidade de calor trocando calor com as redondezas em proporção com o coeficiente de transferência de calor h, a área da superfície A e a diferença de temperatura. Para estruturas na forma de placa, o volume V dividido pela área é simplesmente a espessura da placa para a transferência de calor em um único lado ou a metade da espessura para os dois lados. O sistema atua como um filtro de passa baixa para atenuar as flutuações de temperatura nas redondezas, que ocorrem muito rápido com relação à constante de tempo.
![]()
![]() (8)
(8)
A equação 9 é a função de transferência que explica a deformação térmica induzida resultante das flutuações de temperatura nos arredores numa freqüência ω. Uma confirmação dessa premissa básica vale à pena e exige somente a comparação dos tempos calculados pelas equações 7 e 8.
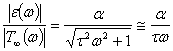 para τω > 1 (9)
para τω > 1 (9)
A tabela 6 mostra as propriedades de alguns materiais e os grupos de propriedades significativos para aço, alumínio, invar-36 e granito natural.
Tabela 6 – Grupos significativos e propriedades para materiais estruturais comuns.
|
Símbolo |
Descrição |
Unidades |
Aço |
Alumínio |
Invar-36 |
Granito |
|
ρ |
Densidade |
Mg/m3 |
7,9 |
2,71 |
8,03 |
2,6 |
|
α |
Coeficiente de expansão térmica |
μm/m/C |
12 |
23 |
1.2 |
6 |
|
κ |
Condutividade |
W/m/C |
54 |
177 |
11 |
4 |
|
C |
Calor específico |
kJ/kg/C |
0,46 |
0,896 |
0,46 |
0,82 |
|
ρC |
Capacidade de calor |
MJ/ m3/C |
3,63 |
2,43 |
3,69 |
2,13 |
|
ρ C/κ=1/D |
Tempo de difusão |
s/mm2 |
0,07 |
0,01 |
0,34 |
0,53 |
|
α/κ |
Expansão sobre condutividade |
μm/W |
0,22 |
0,13 |
0,11 |
1,50 |
|
α /(ρC) |
Atenuada pela convecção |
rel. Aço |
1,00 |
2,87 |
0,10 |
0,85 |
|
ακ /(ρC) |
Atenuada pela condução |
rel. Aço |
1,00 |
9,40 |
0,02 |
0,06 |
O baixo coeficiente de expansão térmica do invar-36 é uma vantagem clara, embora a capacidade do alumínio de conduzir calor quase compense essa vantagem numa situação de fluxo de calor constante. As estruturas de granito atenuam muito bem o erro causado por flutuações de temperatura devido à sua baixa condutividade e sua construção massiva.
A eficiência de um fluido num sistema de controle de temperatura depende primeiramente da sua capacidade calorífica, que é a capacidade de retirar calor, e de seu coeficiente de transferência de calor por convecção. A capacidade de transferir calor aumenta com a velocidade do fluido, mas há um limite prático dado pelo aquecimento viscoso do fluido. Assim, devem ser avaliadas as características de cada fluido antes de selecionar qual é o otimizado para o sistema de controle de temperatura.
Usualmente são empregados a água, o óleo e o ar. A água é claramente superior como meio de controle de temperatura, mas apresenta os sérios problemas de corrosão e evaporação.