4 – Separação de erros sistemáticos
É útil separar os erros de uma máquina-ferramenta em duas categorias, os erros repetitivos e os não-repetitivos. Uma máquina-ferramenta é considerada repetitiva, mas não necessariamente precisa, se desloca uma ferramenta de corte à mesma posição relativa com relação à peça toda vez que for comandada para fazê-lo.
Uma máquina-ferramenta que é repetitiva é muito mais fácil de lidar com relação aos seus erros do que uma que não seja repetitiva. Isto é verdade desde que se esteja procurando uma política de procurar e eliminar fontes de erros, ou compensá-los.
Pode parecer que a idéia de que existem erros repetitivos e não-repetitivos seja inconsistente com o princípio determinístico. Particularmente, um erro aparentemente não repetitivo simplesmente pode não estar relacionado a uma fonte de erros conhecida e esta fonte de erro não estará sob controle. Um erro aparentemente não-repetitivo pode se tornar repetitivo através da determinação de sua relação sistemática com a fonte de erros, ou pode ser reduzido para um nível satisfatório se a sua fonte de erros estiver sob controle ou isolada do sistema. Uma vez que os erros são sistemáticos, sua correção ou compensação dos seus efeitos são meios efetivos de melhorar a precisão da máquina.
Erros aparentemente não-repetitivos possuem fontes que podem ser identificadas, por exemplo, correlacionando os movimentos de uma máquina com mudanças de temperatura no ambiente. Uma vez identificado esse problema, várias ações podem ser tomadas para diminuí-lo.
Um erro sistemático em particular pode ser identificado entre outros erros. Isso requer a realização de testes que sejam sensíveis para determinados tipos de erros e insensíveis a outros, ou pela eliminação das parcelas dos demais erros através de modelos conhecidos.
Erros que existem separadamente numa peça e na máquina de medição serão apresentados combinados num relatório de medição. A separação das parcelas de cada erro requer a realização de calibrações e uma correta manipulação desses resultados obtidos.
Para organizar melhor os erros, Slocum (1991) os dividiu em duas categorias principais, os erros mecânicos quasi-estáticos e os erros causados por forças dinâmicas.
Os erros quasi-estáticos são erros na máquina, sistema de fixação, ferramenta e peça, que ocorrem relativamente devagar. Isso quer dizer que eles ocorrem numa freqüência muito mais baixa do que a banda de movimento que os eixos das máquinas podem utilizar para corrigi-los. Alguns dos erros possuem períodos de horas e até anos, como a fluência em alguns materiais. As fontes desse tipo de erro incluem:
§ Erros geométricos;
§ Erros cinemáticos;
§ Erros induzidos por carregamento externo;
Ø Erros causados por carga gravitacional;
Ø Erros causados pela aceleração dos eixos;
Ø Erros causados pelas forças de corte;
§ Erros induzidos por carregamentos na montagem da máquina;
§ Erros causados por expansão térmica;
§ Erros causados por instabilidade do material;
§ Erros de instrumentação.
Os erros causados por forças dinâmicas provocam vibrações na máquina que se refletem diretamente no acabamento das peças produzidas. Esses erros possuem como principais fontes:
§ Vibrações transmitidas pelo piso;
§ Componentes mecânicos rotativos como motores e transmissões;
§ Mancais rotativos;
§ Ciclos limites em loops dos Servos;
§ Turbulência nas linhas de alimentação de fluidos;
§ Pressão sonora;
§ Instabilidade aerostática em mancais a ar (martelamento pneumático).
De todos os erros apresentados, uma atenção especial deve ser dada aos erros geométricos, que aparecem em todos os componentes individuais da máquina e podem ser afetados por diversos fatores, como:
o Planeza das superfícies;
o Rugosidade das superfícies;
o Pré-carregamento dos mancais;
o Princípios de projeto elástico versus cinemático;
o Filosofias de projeto estrutural.
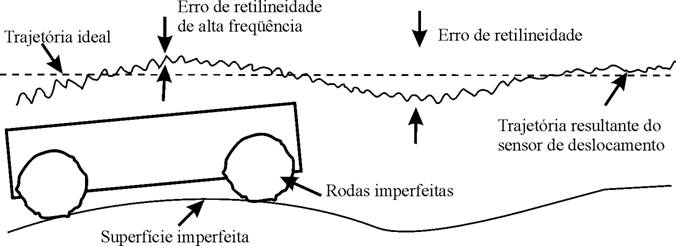
A figura 6 exemplifica os desvios de trajetória que podem ocorrer devido aos erros geométricos combinados por dois componentes de um sistema simples. Se somente dois componentes causam toda essa irregularidade, imagine a composição de erros de diversos componentes.

Figura 6 – Erro numa trajetória retilínea causado pela composição de erros de forma e de acabamento.
Outro erro apresentado que possui uma importância fundamental desde a fase de projeto conceitual da máquina-ferramenta é o erro cinemático. Trata-se de um erro nas trajetórias dos eixos, causado por desalinhamentos e mau dimensionamento dos componentes.
A figura 7 mostra de forma esquemática dois eixos de movimento de uma máquina-ferramenta no plano XZ com um dos eixos alinhado com o eixo de referência X, o erro de ortogonalidade é definido como o desvio εy fora de 90º deste eixo com relação ao outro. Da mesma forma, na figura também estão definidos erros de paralelismo entre eixos.
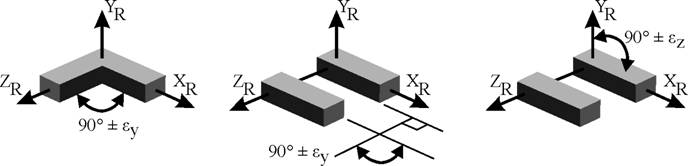
Figura 7 – Erros de ortogonalidade e de paralelismo horizontal e vertical.
Apesar desses erros terem sido divididos com relação às diversas fontes, todos possuem sua parcela sistemática e aleatória. Assim, a separação dessas parcelas é a chave para a compensação desses erros.
A separação de erros sistemáticos expressa várias idéias chaves. Um grande número de técnicas têm sido desenvolvido ao longo dos anos para permitir essa separação. Algumas dessas técnicas são (Hale, 1999):
· Técnicas de reversão (Evans, Hoken e Estler, 1996);
o Reversão por régua padrão;
o Teste dos três planos;
o Reversão ortogonal;
o Reversão Circular de Donaldson (1972);
o Reversão do movimento na face do mancal, de Estler;
· Média de múltiplos passos (Evans e Kestner, 1996);
· Fechamento e subdivisão;
· Autocalibração de padrões 2-D (Raugh, 1997);
· Mapeamento de erro volumétrico (Krulewich, 1998).
Para se ter uma idéia de como funcionam essas técnicas de separação de erros, exemplificamos a técnica de reversão. Essa técnica consiste basicamente em pelo menos dois testes comparativos separados, onde um componente é fisicamente revertido (rotacionado) para mudar o sinal da sua contribuição de erro na medição. Tipicamente, a comparação é efetuada entre uma peça ou padrão e um elemento da máquina. Utiliza-se a peça quando é esta que tem que ser medida, e um padrão quando se quer calibrar a máquina.
O instrumento utilizado para realizar a medição comparativa é sempre denominado um apalpador ou indicador. Deve possuir uma resolução suficiente e ser aferido com relação a um padrão de medição, quando se procura uma medição quantitativa. Geralmente na fabricação, o objetivo é levar essa medição comparativa para o zero, o que não exige um rigor tão grande na aferição do sistema de medição quanto à quantidade medida.
A simetria é um ingrediente chave para todas as técnicas de reversão. O gerador de simetria, tipicamente um eixo de rotação, torna-se efetivamente o artefato perfeito do qual a medição é referenciada. Idealmente, a reversão entre a peça e os instrumentos de medição devem ser perfeitamente simétricos com relação ao gerador de simetria. Uma operação cuidadosa é importante para minimizar desalinhamentos entre os testes, mas as direções desses desalinhamentos são geralmente insensíveis com relação à grandeza medida, tornando-se erros de segunda ordem. Os erros nas direções sensíveis são muito mais críticos para a qualidade da medição.
A reversão depende da máquina e dos instrumentos serem repetitivos e da peça manter a forma constante na região onde passa a trajetória de medição. Geralmente, os testes são feitos de modo que a gravidade permaneça numa direção insensível. Caso não seja possível, um modelamento dos efeitos da gravidade pode fornecer uma base para a compensação dos seus erros.
A reversão por régua padrão requer dois testes comparativos entre uma régua padrão e a guia linear de uma máquina. A régua padrão e a guia da máquina possuem inicialmente erros de retidão desconhecidos, respectivamente S(x) e M(x), esquematizados na figura 8. A régua padrão revertida é mostrada à direita em linhas tracejadas.
O indicador do sistema de medição para os dois testes mede a combinação linear dos erros de retidão I1(x) e I2(x), como especificado na equação 1. Esta escolha determina a convenção de sinal para a retidão de acordo com a leitura do indicador particularmente para um sistema de coordenadas local. Considerando que a guia da máquina é repetitiva e a régua padrão é simétrica entre o primeiro e o segundo testes, então a reversão pode ser considerada como um teste entre uma régua padrão e sua imagem rotacionada, ou entre a guia da máquina e o seu eixo de simetria.
![]()
![]() (1)
(1)
![]() (2)
(2)
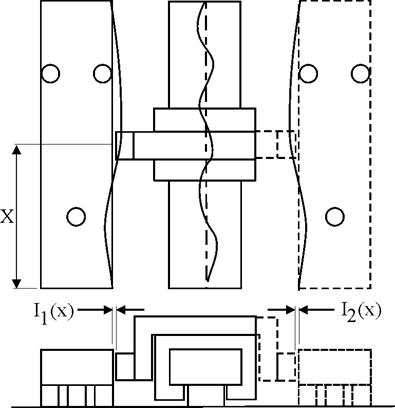
Figura 8 – Esquema de montagem de um teste de reversão por régua padrão.
O embasamento teórico da técnica de reversão por régua padrão é simples, mas algumas considerações devem ser feitas. Existirão inevitavelmente erros de montagem nos testes que exigirão que se considere a retirada das linhas ótimas entre I1(x) e I2(x) ou entre S(x) e M(x), já que elas são combinações lineares. É preferível utilizar um sensor de deslocamento sem contato como sistema de medição, já que este é insensível à sujeira, rugosidade e as diferenças entre os traçados causadas por desalinhamentos. A régua padrão deve ser posicionada de modo a evitar efeitos da gravidade. Além disso, deve-se procurar um traçado na linha média da régua padrão para evitar problemas causados por inclinações da mesma. Efeitos de histerese e tendências são detectados pela medição na direção inversa sobre a mesma trajetória. Usualmente é utilizada a média para ajudar a amortizar a contribuição desses erros na medição de retidão.
Essa técnica exemplificada serve para realizar a reversão com objetivo de avaliar a qualidade de uma trajetória retilínea. Outras técnicas apresentadas por Hale (1999) fornecem base para avaliação de outros parâmetros e outros tipos de trajetórias de componentes em máquinas-ferramenta.
Somente os erros sistemáticos podem ser compensados numa máquina. Mas para se efetuar essa compensação, segundo Sartori (1995), algumas condições devem ser atendidas:
· O erro sistemático a ser compensado deve significativamente maior do que os erros aleatórios;
· As vantagens esperadas da compensação, como o aumento da exatidão da máquina, devem justificar os custos da compensação;
· O erro espacial a ser corrigido deve ser pequena comparada aos intervalos do padrão dimensional utilizado para medir esses erros. Esse ponto clareia as diferenças entre padrões contínuos, como o laser interferométrico, e os padrões descontínuos, como a barra de esferas e placas de esferas utilizadas para a medição dos erros;
· A máquina deve possuir um sistema de coordenadas absoluto. A incerteza na sua origem deve ser menor do que o erro espacial a ser corrigido;
· A performance do controle e dos acionamentos (resolução, freqüência de correção espacial, velocidade de processamento,...) deve ser adequada;
· Um modelo adequado da máquina deve estar disponível, do qual um modelo matemático dos erros, que estabelece as relações funcionais entre as fontes de erros e os erros finais, seja derivado e também do qual os parâmetros de modelo possam ser medidos experimentalmente.
Um modelo de erros simplificado pode reduzir o número de medições a serem feitas para se coletar informações sobre os erros no volume de trabalho da máquina. Por exemplo, numa máquina com volume de trabalho de 1 m3 e com intervalos de coleta de posições relativas de 50 mm, serão necessárias 10000 medições das componentes de erro volumétrico caso não haja um modelo matemático. Além disso, os resultados somente serão válidos se as medições forem obtidas sob as mesmas condições ambientes.
O software de compensação de erros necessita executar um procedimento de três passos:
1. A complexa estrutura da máquina é descrita por um modelo cinemático que deve ser simples, mas deve reproduzir de forma adequada o comportamento real e a performance da máquina. Os aspectos geométricos dessa descrição simplificada são expressos num modelo matemático, o modelo de erro geométrico.
2. Um procedimento experimental é estabelecido para medir, de forma direta ou indireta, os parâmetros do modelo de erro geométrico. Os resultados experimentais são processados, quando necessário, para calcular os parâmetros que caracterizam o modelo de erro geométrico, para finalmente se obter as funções dos erros. A efetividade, isto é, como esses resultados reproduzem o comportamento da máquina, é avaliada.
3. As tabelas ou funções de compensação de erros são construídas e então aplicadas à máquina durante o seu uso para melhorar sua exatidão.
BIBLIOGRAFIA RELACIONADA COM ESTE TÓPICO